Leuke update’s van een van onze projecten Cat Shelter: 1 juli. Helaas blijft kleine Thije op de sukkel. Hij moest in spoed naar de dierenarts die hem grondig onderzocht

Leuke update’s van een van onze projecten Cat Shelter: 1 juli. Helaas blijft kleine Thije op de sukkel. Hij moest in spoed naar de dierenarts die hem grondig onderzocht

Cat Shelter in Limburg is dé kattenopvang voor hulpbehoevende zwerfkatjes die extra verzorging nodig hebben. Namens Cat Shelter Limburg wensen wij u een Vrolijk Pasen.

Twee dagen geleden is dit schattige duifje de vrijheid tegemoet gevlogen. Het jonge duifje, dat uit het nest was gevallen, is met de hand liefdevol grootgebracht door Stichting Vogelasiel te

Dit leuke “echtpaar” moest noodgedwongen verhuizen uit hun vaste stalletje op een kinderboerderij. De bezoekers konden het helaas niet laten hen steeds te voeren met hun meegebrachte brood- en keukenafvallen.

Kleine Imme was bij aankomst erg ziek. Ze heeft in haar jonge leventje al heel hard moeten knokken. Je ziet dat ze op deze foto een katheter draagt, zo kreeg

Helaas komt het nogal eens voor dat vogels tegen ramen vliegen, met als gevolg dat ze eventjes de weg kwijt zijn. In het Vogelasiel in Someren worden ze liefdevol opgevangen.

Onlangs heeft Biedie, die opgevangen was door Stichting De Ezelshoeve, een nieuw thuis èn een nieuwe vriend gevonden. En wat was Chico blij met zijn nieuwe maatje. Het bleek een
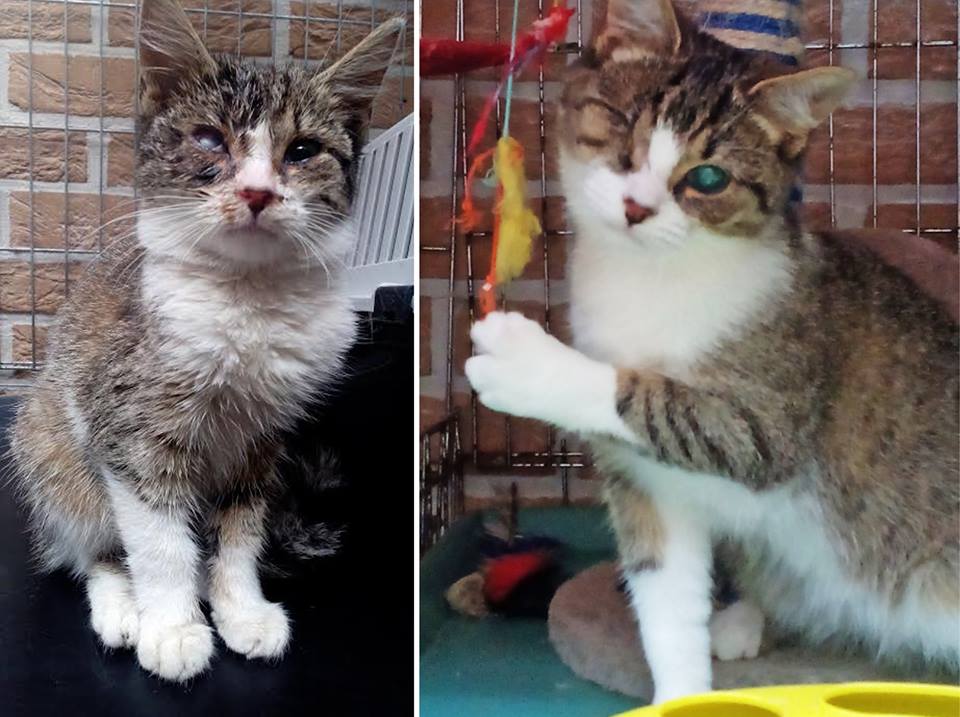
Met Bopper, het leucosepoesje dat graatmager werd gevonden met een slecht oogje gaat het best goed. Het oogje moest helaas verwijderd worden. Het goede nieuws is dat Bopper ondertussen al

De buizerd is waarschijnlijk wel de bekendste Nederlandse roofvogel. Deze buizerd werd onlangs zwaar verzwakt binnengebracht bij de Vogelopvang. Inmiddels kan hij weer zelf eten. Hij wilde helaas niet op

Je kan niet vroeg genoeg beginnen met leren. De Ezelshoeve had deze maand meer dan 80 kleuters op bezoek. Ze werden verteld hoe je met dieren omgaat en hoe je